What is a Force and How to Represent it?

Force

The concept of force can be taken from our daily experience. Although forces cannot be seen or directly observed, we are familiar with their effects. For example, a helical spring stretches when a weight is hung on it or it is pulled. Our muscle tension conveys a qualitative feeling of the force in the spring. Similarly, a stone is accelerated by gravitational force during free fall, or by muscle force when it is thrown. Also, we feel the pressure of a body on our hand when we lift it. Assuming that gravity and its effects are known to us from experience, we can characterize a force as a quantity that is comparable to gravity.

In statics, bodies at rest are investigated. From experience we know that a body subject solely to the effect of gravity falls. To prevent a stone from falling, to keep it in equilibrium, we need to exert a force on it, for example our muscle force. In other words:

A force is a physical quantity that can be brought into equilibrium with gravity.

Characteristics and Representation of a Force

Figure 1

A single force is characterized by three properties: magnitude, direction, and point of application. The quantitative effect of a force is given by its magnitude. A qualitative feeling for the magnitude is conveyed by different muscle tensions when we lift different bodies or when we press against a wall with varying intensities. The magnitude F of a force can be measured by comparing it with gravity, i.e., with calibrated or standardized weights. If the body of weight G in Fig. 1 is in equilibrium, then F = G. The “Newton”, abbreviated N, is used as the unit of force.

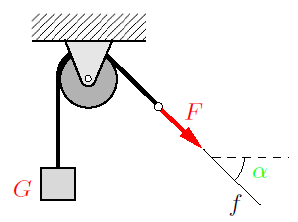
From experience we also know that force has a direction. While gravity always has an effect downwards (towards the earth’s center), we can press against a tabletop in a perpendicular or in an inclined manner. The box on the smooth surface in Fig. 2 will move in different directions, depending on the direction of the force exerted upon it. The direction of the force can be described by its line of action and its sense of direction (orientation). In Fig. 1, the line of action f of the force F is inclined under the angle α to the horizontal. The sense of direction is indicated by the arrow.

Figure 2

Figure 3

Finally, a single force acts at a certain point of application. Depending on the location of point A in Fig. 2, the force will cause different movements of the box. A quantity determined by magnitude and direction is called a vector. In contrast to a free vector, which can be moved arbitrarily in space provided it maintains its direction, a force is tied to its line of action and has a point of application.
Therefore, we conclude:

The force is a bound vector.

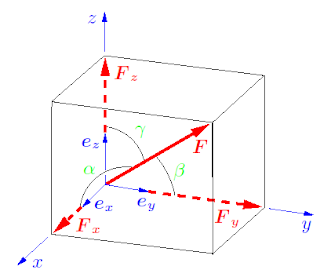
According to standard vector notation, a force is denoted by a boldfaced letter, for example by F, and its magnitude by |F| or simply by F. In figures, a force is represented by an arrow, as shown in Figs. 1 and 2. Since the vector character usually is uniquely determined through the arrow, it is usually sufficient to write only the magnitude F of the force next to the arrow. In Cartesian coordinates (see Fig. 3), the force vector can be represented using the unit vectors e_x, e_y, e_z by,

Applying Pythagorean theorem in space, the force vector’s magnitude F is given by

The direction angles and therefore the direction of the force follow from